5 - Binary Search Tree - 2101667405 - Evania Joycelin A.
1. Operations: Search, Insertion, Deletion
a. Searching for a Node in a Binary Search Tree
- The search function is used to find whether a given value is present in the tree or not.
- The searching process begins at the root node.
- The function first checks if the binary search tree is empty.
- If it is empty, then the value we are searching for is not present in the tree.
- If there are nodes in the tree, then the search function checks to see if the key value of the current node is equal to the value to be searched.
- If not, it checks if the value to be searched for is less than the value of the current node, go to left child node. In case the value is greater than the value of the current node, go to right child node.
 |
| Consider we want to search 12 |
 |
| Consider we want to search 67 |
struct
node* search (struct
node *curr, int X) {
if ( curr == NULL ) return NULL;
// X is found
if ( X == curr->data ) return
curr;
// X is located in left sub tree
if ( X < curr->data ) return
find(curr->left, X);
// X is located in right sub tree
return find(curr->right, X);
}
b. Inserting a New Node in a Binary Search Tree
- The insert function is used to add a new node with a given value at the correct position in the binary search tree.
- The initial code for the insert function is similar to the search function. This is because we first find the correct position where the insertion has to be done and then add the node at that position.
- The insertion function changes the structure of the tree.
- When the insert function is called recursively, the function should return the new tree pointer.
- The insert function checks if the current node of TREE is NULL.
- If it is NULL, the algorithm simply adds the node,
- If the current node’s value is less than that of the new node, then the right sub-tree is traversed, else the left sub-tree is traversed.
- The insert function continues moving down the levels of a binary tree until it reaches a leaf node.
- The new node is added by following the rules of the binary search trees.
- That is, if the new node’s value is greater than that of the parent node, the new node is inserted in the right sub-tree, else it is inserted in the left sub-tree.
 |
| Consider we want to add 12 and 55 |
struct node *insertElement(struct node *tree, int val)
{
struct node *ptr,
*nodeptr, *parentptr;
ptr = (struct
node*)malloc(sizeof(struct node));
ptr–>data =
val;
ptr–>left =
NULL;
ptr–>right =
NULL;
if(tree==NULL)
{
tree=ptr;
tree–>left=NULL;
tree–>right=NULL;
}
else
parentptr=NULL;
nodeptr=tree;
while(nodeptr!=NULL)
{
parentptr=nodeptr;
if(val<nodeptr–>data)
nodeptr=nodeptr–>left;
else
nodeptr
= nodeptr–>right;
}
if(val<parentptr–>data)
parentptr–>left
= ptr;
else
parentptr–>right
= ptr;
}
return tree;
}
c. Deleting a Node from a Binary Search Tree
The delete function deletes a node from the binary search tree. However, utmost care should be taken that the properties of the binary search tree are not violated and nodes are not lost in the process.Case 1: Deleting a Node that has No Children
If we have to delete node 78, we can simply remove this node without any issue. This is the simplest case of deletion.
Case 2: Deleting a Node with One Child
- To handle this case, the node’s child is set as the child of the node’s parent.
- In other words, replace the node with its child.
- Now, if the node is the left child of its parent, the node’s child becomes the left child of the node’s parent.
- if the node is the right child of its parent, the node’s child becomes the right child of the node’s parent.
Case 3: Deleting a Node with Two Children
- To handle this case, replace the node’s value with its in-order predecessor (largest value in the left sub-tree) or in-order successor (smallest value in the right sub-tree).
- The in-order predecessor or the successor can then be deleted using any of the above cases.
- This deletion could also be handled by replacing node 56 with its in-order successor, as shown in above
- We first check if TREE=NULL, because if it is true, then the node to be deleted is not present in the tree.
- However, if that is not the case, then we check if the value to be deleted is less than the current node’s data.
- In case the value is less, we call the algorithm recursively on the node’s left sub-tree, otherwise the algorithm is called recursively on the node’s right sub-tree.
- Note that if we have found the node whose value is equal to VAL, then we check which case of deletion it is.
- If the node to be deleted has both left and right children, then we find the in-order predecessor of the node by calling findLargestNode(TREE -> LEFT) and replace the current node’s value with that of its in-order predecessor.
- Then, we call Delete(TREE -> LEFT, TEMP -> DATA) to delete the initial node of the in-order predecessor.
- Thus, we reduce the case 3 of deletion into either case 1 or case 2 of deletion. If the node to be deleted does not have any child, then we simply set the node to NULL.
- Last but not the least, if the node to be deleted has either a left or a right child but not both, then the current node is replaced by its child node and the initial child node is deleted from the tree.
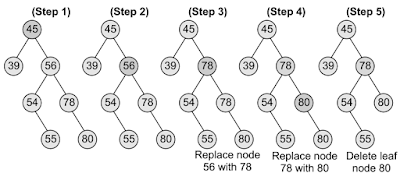 |
| 1. The root is 45 2. Search 56 (it must in the right) 3. Free 56 4. Search in the right who have the greatest value \ 5. Greatest value is 78 9. Replace 56 with 78 |
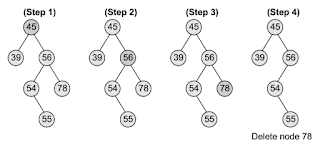
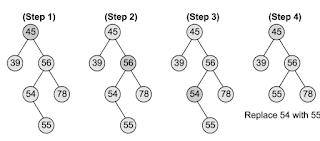






Komentar
Posting Komentar