4 - Introduction to Binary Tree and Expression Tree - 2101667405 - Evania Joycelin A.

1. Tree Concept


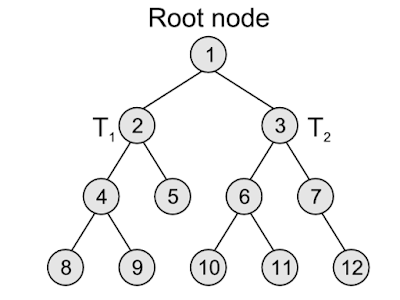
  • Root node The root node R is the topmost node in the tree. If R = NULL, then it means the tree is empty. In the tree above A is the root node
  • Leaf node A node that has no children is called the leaf node or the terminal node. In the tree above E, F, H and I are the leaf node.
  • Ancestor node An ancestor of a node is any predecessor node on the path from root to that node. The root node does not have any ancestors. In the tree above, nodes A, C, and G are the ancestors of node K.
  • Descendant node A descendant node is any successor node on any path from the node to a leaf node. Leaf nodes do not have any descendants. In the tree given in Fig. 9.1, nodes C, G, J, and K are the descendants of node A. 
  • Level number Every node in the tree is assigned a level number in such a way that the root node is at level 0, children of the root node are at level number 1. Thus, every node is at one level higher than its parent.
  • Degree Degree of a node is equal to the number of children that a node has.
  • Nodes that have the same parent are called sibling
  • A line connecting the parent to the child is edge
  • Height/Depth is the maximum degree of nodes in a tree. 

2. Binary Tree Concept

  • A binary tree is a data structure that is defined as a collection of elements called nodes. 
  • Each node has 0, 1, or at the most 2 children. 
  • Every node contains a data element, a left pointer which points to the left child, and a right pointer which points to the right child. 

3. Type of Binary Tree

1. Perfect binary tree is a binary tree in which every level are at the same depth.

2. A complete binary tree is a binary tree that satisfies two properties. First, in a complete binary tree, every level, except possibly the last, is completely filled. Second, all nodes appear as far left as possible.


3. Skewed binary tree is a binary tree in which each node has at most one child


5. Balanced binary tree is a binary tree in which no leaf is much farther away from the root than any other leaf (different balancing scheme allows different definitions of “much farther”).

4. Property of Binary Tree

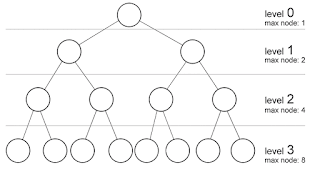
  • Maximum number of nodes on a binary tree of height h is 2h+1 -1 
                           
    Max node of a binary tree of
    height 3
    = 1 + 2 + 4 + 8
    = 20 + 21 + 22 + 23
    = 24 – 1
    = 15
  • In a complete binary tree Tn, there are exactly n nodes and level r of T can have at most 2r nodes
  • Minimum height of a binary tree of n nodes is 2log(n).
    Maximum height of a binary tree of n nodes is n - 1
    Skewed Binary Tree have maximum height

5. Representation of Binary Tree

1. Implementation Using Array
Index on array represents node number
Index 0 is Root node
Index Left Child is 2p + 1, where p is parent index
Index Right Child is 2p + 2
Index Parent is (p-1)/2


2. Implementation Using Linked List
struct node {
  int data;
  struct node *left;
  struct node *right;
  struct node *parent;
};
struct node *root = NULL;

6. Expression Tree Concept


Prefix  : *+ab/-cde
Postfix    : ab+cd-e/*
Infix  : (a+b)*((c-d)/e)






We will use this structure for each node in the tree:
struct tnode {
  char chr;
  struct tnode *left;
  struct tnode *right;
};
It is a binary tree


7. Create Expression from Prefix, Postfix and Infix

1. Prefix

To traverse a non-empty binary tree in pre-order, the following operations are performed recursively at each node. The algorithm works by: 
1. Visiting the root node, 
2. Traversing the left sub-tree, and finally 
3. Traversing the right sub-tree.



Example : 
In Figs (a) and (b), find the sequence of nodes that will be visited using pre-order traversal algorithm.

Solution 
TRAVERSAL ORDER (a): A, B, D, G, H, L, E, C, F, I, J,   and K     

TRAVERSAL ORDER (b): A, B, D, C, E, F, G, H, and I 


We can create an expression tree from a prefix by recursive.
main function

struct tnode *root = newnode(s[0]);
f(root);

char s[MAXN];
int  p = 0;
void f(struct tnode *curr) {
  if ( is_operator(s[p]) ) {
  p++; curr->left  = newnode(s[p]);
  f(curr->left);
  p++; curr->right = newnode(s[p]);
  f(curr->right);
  }
}

Doing a prefix or postfix traversal in an expression tree is simple.
void prefix(struct tnode *curr) {
  printf( “%c “, curr->chr );
  if ( curr->left  != 0 ) prefix(curr->left);
  if ( curr->right != 0 ) prefix(curr->right);
}
In prefix, you have to print/process before its child are processed

2. Postfix 

To traverse a non-empty binary tree in post-order, the following operations are performed recursively at each node. 
The algorithm works by: 
1. Traversing the left sub-tree, 
2. Traversing the right sub-tree, and finally 
3. Visiting the root node

TRAVERSAL ORDER: G, L, H, D, E, B, I, K, J, F, C, and A 

TRAVERSAL ORDER: D, B, H, I, G, F, E, C, and A








void postfix(struct tnode *curr) {
  if ( curr->left  != 0 ) postfix(curr->left);
  if ( curr->right != 0 ) postfix(curr->right);
  printf( “%c“, curr->chr );
}
In postfix, you have to print/process after its child have been processed.

3. Infix

How about infix? Can we just do like this code below?
void infix(struct tnode *curr) {
  if ( curr->left  != 0 ) infix(curr->left);
  printf( “%c“, curr->chr );
  if ( curr->right != 0 ) infix(curr->right);
}

Wrong infix  : a+b*c
Correct infix  : (a+b)*c














To fix that, we can add brackets () when expanding an operator.

void infix(tnode *curr) {
  if ( is_operator(curr->chr) ) putchar( '(' );
  if ( curr->left != 0 ) infix(curr->left);
  printf( "%c", curr->chr );
  if ( curr->right != 0 ) infix(curr->right);
  if ( is_operator(curr->chr) ) putchar( ')' );
}

So * + a b c in prefix will be encoded as ((a + b) * c) in infix, which is correct.
References: Reema Thareja,. 2014. Data structures using C. OXFOR. New Delhi. ISBN:978-0-19-809930-7 Chapter 9 & 10

Komentar

Posting Komentar

Postingan Populer