3 - Linked List Implementation II - 2101667405 - Evania Joycelin A.
1. Stack Concept
- Stack is an important data structure which stores its elements in an ordered manner.
- This is the analogy: You must have seen a pile of plates where one plate is placed on top of another as shown in picture below. Now, when you want to remove a plate, you remove the topmost plate first.
- A stack is a linear data structure which uses the same analogy above, the elements in a stack are added and removed only from one end, which is called the TOP.
- A stack is called a LIFO (Last-In-First-Out) data structure, as the element that was inserted last is the first one to be taken out.
- We need stacks in computer science in function calls. Consider an example, where we are executing function A. In the course of its execution, function A calls another function B. Function B in turn calls another function C, which calls function D.
2. Array Representation
- In the computer’s memory, stacks can be represented as a linear array.
- Stack has 2 Variable:
- TOP which is used to store the address of the topmost element of the stack. It is this position where the element will be added to or deleted from.
- MAX, which is used to store the maximum number of elements that the stack can hold. If TOP = NULL, then it indicates that the stack is empty and if TOP = MAX–1, then the stack is full.
Picture above shows that TOP = 4, so insertions and deletions will be done at this position. In the above stack, five more elements can still be stored.
3. Linked List Representation
- If the array size cannot be determined in advance, then the other alternative. Linked representation, is used.
- In a linked stack, every node has two parts—one that stores data and another that stores the address of the next node.
- The START pointer of the linked list is used as TOP. All insertions and deletions are done at the node pointed by TOP.
- If TOP = NULL, then it indicates that the stack is empty.
4. Stacks Operation
1. PUSH
- The push operation is used to insert an element into the stack.
- The new element is added at the topmost position of the stack.
- Before inserting the value, we must first check if TOP=MAX–1, because if that is the case, then the stack is full and no more insertions can be done. If an attempt is made to insert a value in a stack that is already full, an OVERFLOW message is printed.
- To insert an element with value 6, we first check if TOP=MAX–1. If the condition is false, then we increment the value of TOP and store the new element at the position given by stack[TOP]
2. POP
- The pop operation is used to delete the topmost element from the stack.
- Before deleting the value, we must first check if TOP=NULL because if that is the case, then it means the stack is empty and no more deletions can be done. If an attempt is made to delete a value from a stack that is already empty, an UNDERFLOW message is printed.
- Stack To delete the topmost element, we first check if TOP=NULL. If the condition is false, then we decreament the value pointed by TOP.
3. PEEK/TOP
- Peek is an operation that returns the value of the topmost element of the stack without deleting it from the stack.
- However, the Peek operation first checks if the stack is empty. If TOP = NULL, then an appropriate message is printed, else the value is returned.
5. Stack Application
There
are several applications using stack data structure
that we will discuss:
- Reversing a list
- Parentheses checker
- Conversion of an infix expression into a postfix expression
- Evaluation of a postfix expression
- Conversion of an infix expression into a prefix expression
- Evaluation of a prefix expression
- Recursion
- Tower of Hanoi
- Infix evaluation
- Depth First Search
- Infix to Prefix conversion
- Infix to Postfix conversion
- Prefix evaluation
- Postfix evaluation
6. Infix, Postfix and Prefeix Notation
1. Postfix/Polish Notation
But before learning about prefix and postfix notations, let us first see what an infix notation is. We all are familiar with the infix notation of writing algebraic expressions. While writing an arithmetic expression using infix notation, the operator is placed in between the operands. For example, A+B.
Although it is easy for us to write expressions using infix notation, computers find it difficult to parse as the computer needs a lot of information to evaluate the expression. Information is needed about operator precedence and associativity rules, and brackets which override these rules.
- Postfix notation was developed by Jan Łukasiewicz who was a Polish logician, mathematician, and philosopher.
- In postfix notation, as the name suggests, the operator is placed after the operands.
- The order of evaluation of a postfix expression is always from left to right. Even brackets cannot alter the order of evaluation.
- A postfix operation does not even follow the rules of operator precedence.
How To Convert Infix notation to Postfix notation?
- Write priority operator first
- Write the left operand from the operator
- write the right operand from the operator
Example in (a) we have + as the priority operator (because it has braces) then we write A as the left operand and then B as the right operand. Now suppose that +AB (that we have covert to postfix notation) is a one operand, so we write * first then +AB as the left operand and C as the right operand.
Evaluate The Postfix Notation
- Using stacks, any postfix expression can be evaluated very easily.
- Every character of the postfix expression is scanned from left to right.
- If the character encountered is an operand, it is pushed on to the stack. However, if an operator is encountered, then the top two values are popped from the stack and the operator is applied on these values.
- The result is then pushed on to the stack.
2. Prefix Notation
How To Convert Infix notation to Postfix notation
- Write the left operand from the operator
- write the right operand from the operator
- Write the priority operator
Example (A-B)*(C-D). Scanning from left to the right, we have (A-B) to be solve first then (C-D) then we multiply them. So write A first as the left operand, then B as the right operand then write the operator - (AB-). Then write C as the left operand then write D as the right operand then write the operator -(CD-). After that assume that (AB-) is a one operand also (CD-), so we just put the / in behind. (AB-CD-/)
Evaluate The Prefix Notation
For example, consider the prefix expression + – 9 2 7 * 8 / 4 12
7. Depth First Search
Depth First Search (DFS) is an algorithm for traversing or searching in a tree or graph. We start a the root of the tree (or some arbitrary node in graph) and explore as far as possible along each branch before backtracking.
DFS has many applications, such as:
• Finding articulation point and bridge in a graph
• Finding connected component
• Topological sorting
DFS can be implemented by a recursive function or an iterative procedure using stack, their results may have a little differences on visiting order but both are correct.
Algorithm:
Prepare an empty stack
Push source/root into stack
Mark source/root
While stack is not empty
Pop an item from stack into P
For each node X adjacent with P
If X is not marked
Mark X
Push X into stack
Visit
order: A, C, B, E, D
8. Breadth First Search
Breadth First Search (BFS) like DFS is also an algorithm for traversing or searching in a tree or graph.
We start at the root of the tree (or some arbitrary node in graph) and explore all neighboring nodes level per level until we find the goal.
We start at the root of the tree (or some arbitrary node in graph) and explore all neighboring nodes level per level until we find the goal.
BFS has many applications, such as:
- Finding connected component in a graph.
- Finding shortest path in an unweighted graph.
- Ford-Fulkerson method for computing maximum flow.
Algorithm:
Prepare an empty queue
Push source/root into queue
Mark source/root
While queue is not empty
Pop an item from queue into P
For each node X adjacent with P
If X is not marked
Mark X
Push X into queue
9. Queue
Queue is an important data structure which stores its elements in an ordered manner
Example:
- People moving on an escalator. The people who got on the escalator first will be the first one to step out of it.
- People waiting for a bus. The person standing in the line will be the first one to get into the bus
- Luggage kept on conveyor belts
- Cars lined for filling petrol
- Cars lined at a toll bridged
Queue can be implemented by either using arrays or linked lists.
The elements in a queue are added at one end called the rear and removed from the other one end called front.
The data are stored in First In First Out (FIFO) way, this is the main difference between stack and queue.
1. Array Representation
• Queue has two variables:
– Front and rear
that point to the position where deletions and insertions can be done
respectively
•Here, front = 0 and rear = 5.
2. Linked List Representation
•
Similar
with stack, technique of creating a queue using array is easy, but its drawback
is that the array must be declared to have some fixed size.
•
In
a linked queue, every element has two parts
– One that stores the data
– Another that stores the address of
the next element
•
The
START pointer of the linked list is used as the FRONT
•
All
insertions will be done at the REAR, and all the deletions are done at the
FRONT end.
•
If
FRONT = REAR = NULL, then it indicates that the queue is empty
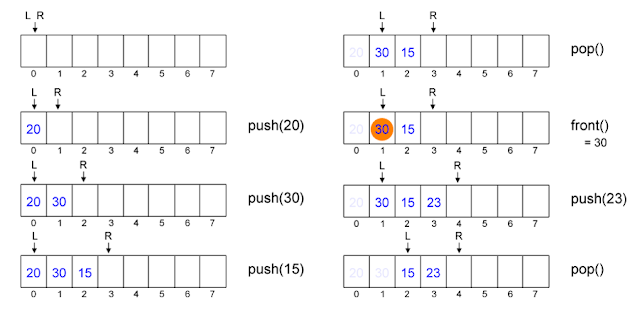
3. Queue Operations
•
push(x) : add an item x to the back of the
queue.
•
pop() : remove an item from the front of
the queue.
•
front() : reveal/return the
most front item from the queue. (peek)
4. Circular Queue
- We can wrap-around index L and R.
- If R reach MAXN then set R as zero, do the same to L.
- It is also known as circular queue.
5. Deques
- A deque (pronounced as ‘deck’ or ‘dequeue’) is a list in which elements can be inserted or deleted at either end.
- It is also known as a head-tail linked list, because elements can be added to or removed from the front (head) or back (tail).
Two variants of a
double-ended queue, include:
· Input restricted deque
In this dequeue insertions can be done only at one of the
dequeue while deletions can be done from both the ends.
· Output restricted deque
· In this dequeue deletions can be done only at one of the
dequeue while insertions can be done on both the ends.
6. Priority Queue
A priority
queue is an abstract
data type in which the each element is assigned a priority.
The general rule
of processing elements of a priority queue can
be given as:
•
An
element with higher priority is processes before an element with lower priority
•
Two
elements with same priority are processed on a first come first served (FCFS)
basis
Deletion:
•
Deletion
is a very simple process in this case. The first node of the
•
list
will be deleted and the data of that node will be processed first




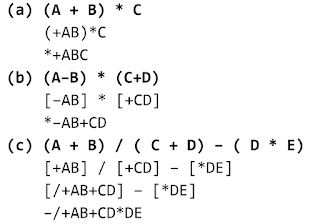











Komentar
Posting Komentar